This problem involves using recursion to solve the 0-1 Knapsack, which may result in a Time Limit Exceeded (TLE) error.
Contents
- Imagine you're once again a thief in an electronics shop, but unlike with fractional knapsack, this time you can only steal either the entire item or none of it; you can't take a fraction of an item.
- Everything else is similar to Fractional Knapsack.
Base Case.
Recursively explore all possible outcomes and return the case with the
maxProfit.1. Base Case
Consider scenarios where the thief ends up with 0
maxProfit:- He forgot to bring his bag or the capacity of the bag is 0 (
capacity == 0). - The shop is already empty (
N == 0), whereNis the size of theItemarray.
2. Recursive Relation
Case 1 :
If an item's weight is less than the knapsack's capacity, it can either be included in the knapsack or left out, based on its profit-to-weight ratio(based on potential profit).
Using the principle of recursion, we can solve the knapsack problem by considering only one item at a time. The recursive function will automatically handle the remaining items.
max(arr[N-1].value + KnapSack(arr, N-1, capacity - arr[N-1].weight), KnapSack(arr, N-1,capacity));Compares the profit with and without the current item, returning the maximum.
Case 2 :
If the item doesn't meet the criteria, proceed to the next index by reducing the size:
KnapSack(arr, N-1, capacity)
- He forgot to bring his bag or the capacity of the bag is 0 (
Again each item is stored as {weight,profit}
Item arr[] = {{2,30},{3,50},{6,30}};
capacity = 5
| Item | Weight | Profit |
|---|---|---|
| A | 2 | 30 |
| B | 3 | 50 |
| C | 6 | 30 |
Output : 80
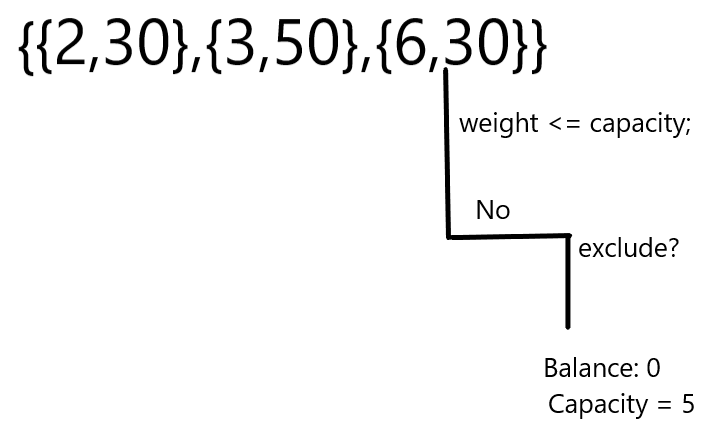
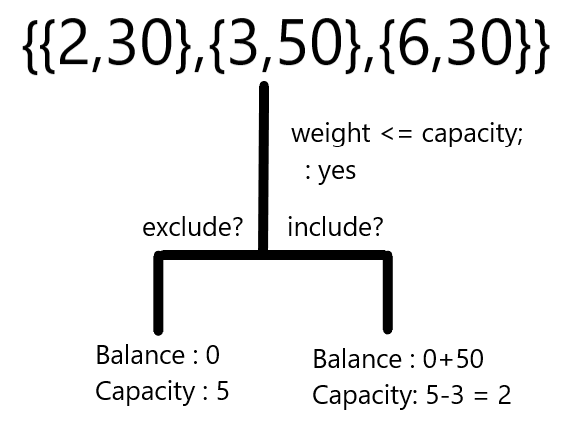
- Checking the last element(N = 2)
- Checking N-1 (N = 1)
- Checking N-1 (N = 0)
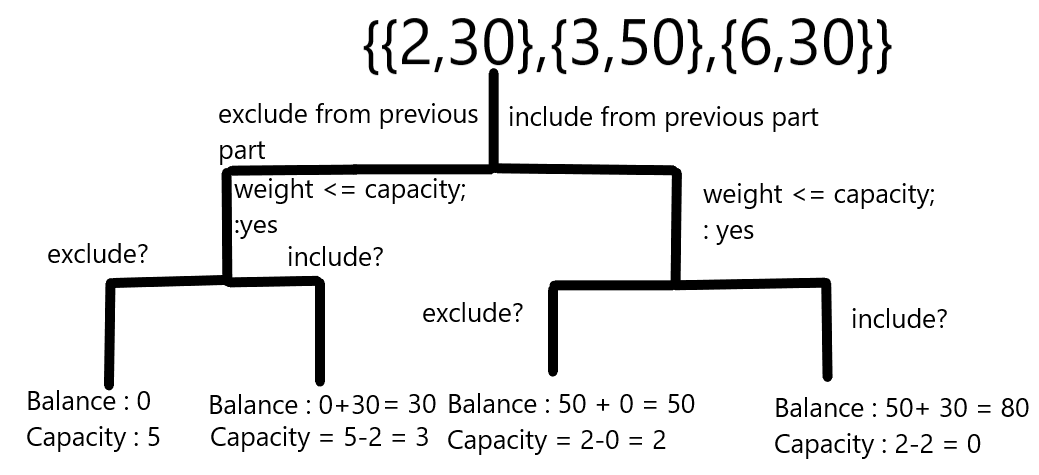
Hence, the output is 80
max(include,exclude);
From above example we can easily see that with only 4 items there are these many recursive calls thus it can it can result in TLE for multiple inputs.
#include <iostream>
using namespace std;
class Item
{
public:
int weight;
int value;
Item(int weight, int value)
{
this->value = value;
this->weight = weight;
}
};
int KnapSack(Item arr[], int N , int capacity)
{
//base-case
if(N == 0 || capacity == 0)
{
return 0;
}
//recursive-function
if(arr[N-1].weight <= capacity)
{
int case1 = arr[N-1].value + KnapSack(arr,N-1,capacity-arr[N-1].weight);
int case2 = KnapSack(arr,N-1,capacity);
return max(case1,case2);
}
else if(arr[N-1].weight > capacity)
{
return KnapSack(arr,N-1,capacity);
}
}
int main()
{
Item arr[] = {{1,20},{2,30},{3,30},{4,50}};
int N = sizeof(arr)/sizeof(arr[0]);
int capacity;
cout << "Enter the capacity : ";
cin >> capacity;
cout << KnapSack(arr,N,capacity);
}
0-1 KnapSack Code
int KnapSack(Item arr[], int N , int capacity)
{
//base-case
if(N == 0 || capacity == 0)
{
return 0;
}
//recursive-function
if(arr[N-1].weight <= capacity)
{
int case1 = arr[N-1].value + KnapSack(arr,N-1,capacity-arr[N-1].weight);
int case2 = KnapSack(arr,N-1,capacity);
return max(case1,case2);
}
else if(arr[N-1].weight > capacity)
{
return KnapSack(arr,N-1,capacity);
}
}
- Base Cases are already explained in Algorithm
- If
(arr[N-1].weight <= capacity):- Then we can either include it or exclude it
- Include(case1) :
arr[N-1].value + KnapSack(arr,N-1,capacity-arr[N-1].weight);
- Exclude(case2) :
KnapSack(arr,N-1,capacity)
- Include(case1) :
- The Final Output will be
max(case1, case2);
- Then we can either include it or exclude it
- If
arr[N-1].weight > capacity- Then we can directly exclude the item